Red black trees in F#

Red-black trees

Days ago when I was browsing the Internet, I came across a gitbook tutorial on how to implement specific data structures in OCaml, which included red-black trees. Red-black trees are a type of self-balancing binary search trees that could keep its worst case search/insertion/deletion time within $O(\log(N))$. If you are looking for a complete introduction to what red-black trees are, you may refer to its Wikipedia page. As I have been looking into F# and .NET for quite some time, I thought it might be good practice to implement the data structure in F#.

Nodes in the red-black trees are painted in either red or black, which gives our definition to the Color and RedBlackTree types.

[<Struct>]
type Color =
	| Red
	| Black
type 'a RedBlackTree =
	| Node of Color * 'a * 'a RedBlackTree * 'a RedBlackTree
	| Leaf

Insertion

The reason why insertions and deletions to elements in a red-black tree are complicated is that we must maintain the local and global invariants of the data structure after making changes to it. Naively adding or removing tree nodes could potentially cause connections between two red nodes or break the equality of number of black nodes among all paths.

For the implementation of insertions to our red-black trees, we follow the method proposed by Okasaki, which first inserts a red node to the corresponding location on the fringe of the tree (if the element was previously absent in the tree), then moves up to the root while applying rotations to resolve violations to the local invariant (connection between red nodes). Finally, the algorithm paints the root of the red-black tree black in case it was painted red during the last rotation.

Violations to the local invariant could appear in one of these four configurations:

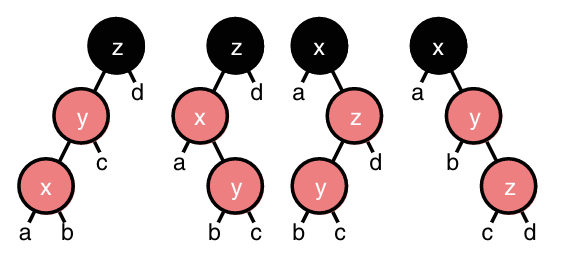
After our rotation, we want to obtain this:

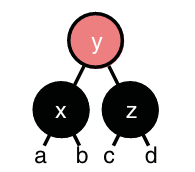
The corresponding F# implementation would be:

let balance = function
    | Node(Black, z, Node(Red, y, Node(Red, x, a, b), c), d)
    | Node(Black, z, Node(Red, x, a, Node(Red, y, b, c)), d)
    | Node(Black, x, a, Node(Red, y, b, Node(Red, z, c, d))) ->
        Node(Red, y, Node(Black, x, a, b), Node(Black, z, c, d))
    | n -> n

let insert (x: 'a) (t: 'a RedBlackTree) : 'a RedBlackTree =
    let rec ins = function
        | Leaf Black -> Node(Red, x, Leaf Black, Leaf Black)
        | Node(color, y, a, b) as s ->
            if x < y then balance (Node(color, y, ins a, b))
            elif x > y then balance (Node(color, y, a, ins b))
            else s
        | _ -> failwith "unreachable"
    match ins t with
    | Node(_, y, a, b) -> Node(Black, y, a, b)
    | _ -> failwith "unreachable"

The balance function works to resolve the violations demonstrated above. The insert function first calls the recursive function ins to search for the proper location to add the new node, then traverses from the node up to the root while making rotations.

Deletion

Deletion is in some ways dual to insertions to the red-black trees. Removal to nodes are only made on the presence of the indicated elements, whereas in insertions changes are made only on the absence of the elements. However, insertions would only affect nodes on the fringe, while deletions could remove internal nodes, which makes it harder to maintain the local and global invariants.

Kimball Germane and Matthew Might suggested a method by adding a temporary color “double-black”. Double-black nodes are counted twice when checking the global invariant. Notice that both internal nodes and leaves of the tree could be painted double-black, so we must make changes to our definition of the red-black tree.

[<Struct>]
type Color =
    | Red
    | Black
    | DoubleBlack

type 'a RedBlackTree =
    | Node of Color * 'a * 'a RedBlackTree * 'a RedBlackTree
    | Leaf of Color

The algorithm first considers the cases where the removed node is indeed on the fringe. Then for the cases where the nodes to remove are internal, it would swap it with its successor in the in-order traversal of the tree. Since this successor node contains the smallest element of the current node’s right subtree, it must be located on the fringe. In this way, we are able to avoid the problem of deleting internal nodes directly.

For detail of this algorithm, please refer to their paper: Deletion: The curse of the red-black tree.

let balance = function
    | Node(Black, z, Node(Red, y, Node(Red, x, a, b), c), d)
    | Node(Black, z, Node(Red, x, a, Node(Red, y, b, c)), d)
    | Node(Black, x, a, Node(Red, y, b, Node(Red, z, c, d))) ->
        Node(Red, y, Node(Black, x, a, b), Node(Black, z, c, d))
    | Node(DoubleBlack, z, Node(Red, x, a, Node(Red, y, b, c)), d)
    | Node(DoubleBlack, x, a, Node(Red, z, Node(Red, y, b, c), d)) ->
        Node(Black, y, Node(Red, x, a, b), Node(Red, z, c, d))
    | n -> n

let rotate = function
    // case 1:
    | Node(Red, y, Node(DoubleBlack, x, a, b), Node(Black, z, c, d)) ->
        balance <| Node(Black, z, Node(Red, y, Node(Black, x, a, b), c), d)
    | Node(Red, y, Leaf DoubleBlack , Node(Black, z, c, d)) ->
        balance <| Node(Black, z, Node(Red, y, Leaf Black , c), d)
    // reflection of case 1:
    | Node(Red, y, Node(Black, x, a, b), Node(DoubleBlack, z, c, d)) ->
        balance <| Node(Black, x, a, Node(Red, y, b, Node(Black, z, c, d)))
    | Node(Red, y, Node(Black, x, a, b), Leaf DoubleBlack) ->
        balance <| Node(Black, x, a, Node(Red, y, b, Leaf Black))
    // case 2:
    | Node(Black, y, Node(DoubleBlack, x, a, b), Node(Black, z, c, d)) ->
        balance <| Node(DoubleBlack, z, Node(Red, y, Node(Black, x, a, b), c), d)
    | Node(Black, y, Leaf DoubleBlack, Node(Black, z, c, d)) ->
        balance <| Node(DoubleBlack, z, Node(Red, y, Leaf Black, c), d)
    // reflection of case 2:
    | Node(Black, y, Node(Black, x, a, b), Node(DoubleBlack, z, c, d)) ->
        balance <| Node(DoubleBlack, x, a, Node(Red, y, b, Node(Black, z, c, d)))
    | Node(Black, y, Node(Black, x, a, b), Leaf DoubleBlack) ->
        balance <| Node(DoubleBlack, x, a, Node(Red, y, b, Leaf Black))
    // case 3:
    | Node(Black, x, Node(DoubleBlack, w, a, b), Node(Red, z, Node(Black, y, c, d), e)) ->
        Node(Black, z, Node(Black, y, Node(Red, x, Node(Black, w, a, b), c), d), e)
    | Node(Black, x, Leaf DoubleBlack, Node(Red, z, Node(Black, y, c, d), e)) ->
        Node(Black, z, Node(Black, y, Node(Red, x, Leaf Black, c), d), e)
    // reflection of case 3:
    | Node(Black, y, Node(Red, w, a, Node(Black, x, b, c)), Node(DoubleBlack, z, d, e)) ->
        Node(Black, w, a, Node(Black, x, b, Node(Red, y, c, Node(Black, z, d, e))))
    | Node(Black, y, Node(Red, w, a, Node(Black, x, b, c)), Leaf DoubleBlack) ->
        Node(Black, w, a, Node(Black, x, b, Node(Red, y, c, Leaf Black)))
    | n -> n

let delete (x: 'a) (t: 'a RedBlackTree) : 'a RedBlackTree =
    let rec delMin = function
        | Node(Red, y, Leaf Black, Leaf Black) -> y, Leaf Black
        | Node(Black, y, Leaf Black, Leaf Black) -> y, Leaf DoubleBlack
        | Node(Black, y, Leaf Black, Node(Red, z, a, b)) -> y, Node(Black, z, a, b)
        | Node(color, y, a, b) ->
            let z, a' = delMin a
            z, rotate <| Node(color, y, a', b)
        | _ -> failwith "unreachable"
        
    let rec del = function
        | Leaf Black -> Leaf Black
        | Node(Red, y, Leaf Black, Leaf Black) when x = y -> Leaf Black
        | Node(Black, y, Node(Red, z, a, b), Leaf Black) when x = y -> Node(Black, z, a, b)
        | Node(Black, y, Leaf Black, Leaf Black) when x = y -> Leaf DoubleBlack
        | Node(color, y, a, b) ->
            if x < y then rotate <| Node(color, y, del a, b)
            elif x > y then rotate <| Node(color, y, a, del b)
            else
                let z, b' = delMin b
                rotate <| Node(color, z, a, b')
        | _ -> failwith "unreachable"
    match del t with
    | Node(_, y, a, b) -> Node(Black, y, a, b)
    | Leaf _ -> Leaf Black

Reference

• Okasaki, C. (1999) Red-black trees in a functional setting. J. Funct. Program. 9(04), 471–477.
• Germane, K., & Might, M. (2014). Deletion: The curse of the red-black tree. J. Funct. Program. 24(4), 423–433.